§ 1.7 Аэродинамические моментыМомент относительно ц.м. от действующей на БР
силы возникает, как известно из
теоретической механики, в случае, когда
линия действия силы не проходит через ц.м.
ракеты. Тяга двигателя не будет создавать
момента относительно ц.м., если поворотные
камеры сгорания находятся в исходном в исходном
положении и двигатель абсолютно точно установлен
на ракете. Если же отклонить поворотные камеры
сгорания на некоторый угол, то возникнет момент,
называемый управляющим моментом |
|
Статический аэродинамический момент Статический аэродинамический момент Вращательное движение БР удобно рассматривать
относительно осей связанной СК
(Рис. 1.11). Положение ц.м. БР точки S и
ц.д. точки Д будем определять расстояниями
1) |
| Рис. 1.11 |
Из
Рис. 1.11 следует, что осевая составляющая
силы Составляющие Y и Z создают относительно ц.м. моменты |
|
или
где
Здесь Значения сил Y и Z были получены ранее (см. (1.39)). На основании выражений (1.39), (1.40) и (1.41) можно записать |
(1.41) |
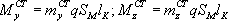 где |
(1.42) |
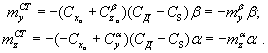 здесь Из выражений (1.43) следует, что аэродинамические коэффициенты составляющих статического момента при малых значениях углов атаки и скольжения имеют линейную зависимость от значений этих углов. Иногда для составляющих статического момента используют выражения: 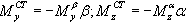 где |
(1.43) |
| Рис. 1.12 |
При расположении ц.д. позади ц.м.
момент При расположении ц.д. впереди ц.м. статический момент действует в сторону увеличения углов атаки и скольжения, стремится как бы опрокинуть БР и поэтому называется опрокидывающим моментом, а ракета в этом случае назвается статически неустойчивой (Рис. 1.12, б). |
|
Демпфирующие моменты Демпфирующими моментами называют моменты, которые возникают при угловом вращении БР и направлены в сторону, противоположную ее вращению. Они демпфируют (тушат) моменты, вызывающие свое появление. Величина демпфирующего момента зависит от условий обтекания корпуса БР потоком воздуха и от условий движения жидкости и газов внутри корпуса БР и двигателя. В соответствии с этим различают внешний (аэродинамический) и внутренний демпфирующие моменты. Аэродинамический демпфирующий момент
|
|
|
| Рис. 1.12 |
Допустим, что корпус БР совершает помимо
поступательного движения со скоростью
V и вращательное движение вокруг оси SZ
со
скоростью
С учетом малости угла Наличие угла С учетом выражения (1.44) перепишем момент в виде: Полная величина демпфирующего момента равна интегралу элементарных моментов, взятому по всей длине корпуса БР и вычисляется по известной из аэродинамики формуле []: |
(1.44)
|
|
где
В полете БР совершает сложное вращение, в
котором вектор 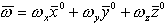 , ,
где Пользуясь выражением (1.47), запишем составляющие демпфирующего момента по осям связанной СК: 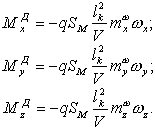 или короче 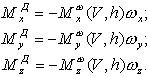 где Для осесимметричного БР справедливо равенство Внутренний демпфирующий момент. Наряду с внешним (аэродинамическим) демпфирующим моментом существует внутренний демпфирующий момент. Он обусловлен наличием кориолисовых ускорений, которые возникают при вращении вместе с БР, компонентов топлива, протекающего по трубопроводам и бакам БР. Газовая струя, истекающая из двигателя, также приводит к появлению внутреннего демпфирующего момента. Внутренний демпфирующий момент приобретает существенное значение при движении БР вне атмосферы. |
(1.45) |
| в начало | << § 1.6 | оглавление | § 1.8 >> |
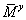 .
Сила притяжения Земли не создает момента
относительно ц.м., так как ц.м. является точкой
ее приложения к БР. Аэродинамическая сила,
приложенная в ц.д., который в общем случае не
совпадает с ц.м. ракеты, создает
аэродинамический момент, который представляют в
виде суммы статического аэродинамического
момента
.
Сила притяжения Земли не создает момента
относительно ц.м., так как ц.м. является точкой
ее приложения к БР. Аэродинамическая сила,
приложенная в ц.д., который в общем случае не
совпадает с ц.м. ракеты, создает
аэродинамический момент, который представляют в
виде суммы статического аэродинамического
момента 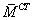 и
деформирующего момента
и
деформирующего момента  .
.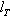

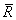 сила X действует вдоль продольной
оси и поэтому не создает момента относительно
ц.м., то есть
сила X действует вдоль продольной
оси и поэтому не создает момента относительно
ц.м., то есть 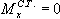 .
.
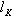 —
—  — безразмерные аэродинамические коэффициенты
статических моментов;
— безразмерные аэродинамические коэффициенты
статических моментов; 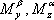 — градиенты статистического аэродинамического
момента. В случае осевой симметрии БР
— градиенты статистического аэродинамического
момента. В случае осевой симметрии БР 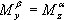 .
.
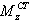
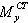
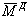 возникает вследствие сопротивления воздушной
среды повороту корпуса БР вокруг ее ц.м.
возникает вследствие сопротивления воздушной
среды повороту корпуса БР вокруг ее ц.м.
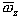
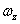 и
расстоянию
и
расстоянию
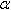 ,
то выделенный элемент поверхности находится к
потоку под местным углом атаки
,
то выделенный элемент поверхности находится к
потоку под местным углом атаки  .
.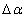 можно
записать
можно
записать  ,
откуда:
,
откуда:
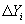 , которая, действуя на
, которая, действуя на 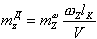 - безразмерный аэродинамический коэффициент
демпфирующего момента;
- безразмерный аэродинамический коэффициент
демпфирующего момента; 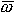 не совпадает ни с одной из осей связанной
системы координат. В этом случае он может
быть представлен в виде суммы трех
составляющих по осям связанной системы
координат:
не совпадает ни с одной из осей связанной
системы координат. В этом случае он может
быть представлен в виде суммы трех
составляющих по осям связанной системы
координат:
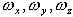 - проекции вектора
- проекции вектора  - единичные векторы осей связанной СК .
- единичные векторы осей связанной СК .
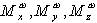 - градиенты составляющих демпфирующего момента.
- градиенты составляющих демпфирующего момента.
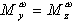 .
.