§ 1.4 Сила тяжести и ее потенциал. Ускорение свободного паденияСила тяжести Данное выражение справедливо как для сферической, так и для эллипсоидальной моделей Земли. На Рис. 1.5 показана сферическая модель Земли. Рассмотрим ниже общий случай эллипсоидальной модели Земли. Сила инерции переносного движения является консервативной силой и имеет силовую функцию. Следовательно, потенциал силя тяжести эллипсоидальной Земли равен |
 , ,
где Переносное ускорение определяется следующей зависимостью: |
(1.16) |

где Потенциал силы инерции переносного движения может быть получен, если воспользоваться его свойством, согласно которому производная от потенциала силы по какому-либо направлению равна проекции этой силы на данное направление. Для единичной массы сила равна ускорению |
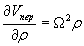 откуда потенциал силы инерции переносного движения равен 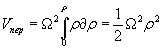 |
| Рис. 1.4 |
Учитывая, что |
 В соответствии с выражением (1.16) потенциал силы тяжести эллипсоидальной Земли можно выразить зависимостью: |
(1.17) |
 По аналогии с выводами (1.14), (1.15) составляющие ускорения свободного
падения на направления 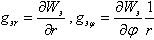 или |
(1.18) |
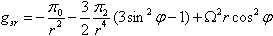 |
(1.19) |
 |
(1.20) |
|
Из выражений (1.19)
и (1.20) следует,
что сила тяжести на эллипсоиде не является центральной силой, и угол,
заключенный между линией действия силы тяжести (линией отвеса) и плоскостью
экватора, будет больше, чем угол между радиусом-вектором |
| Рис. 1.5 |
Иногда при расчетах удобнее пользоваться не составляющими
(1.19) и (1.20),
а неортогональными проекциями ускорения свободного падения на направление
радиуса-вектора |
|
Разложим меридианальную составляющую ускорения Учитывая выражение (1.20), получаем  Составляющая |
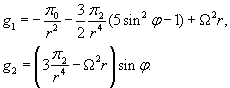
Составляющая |
(1.21) |
| в начало | << § 1.3 | оглавление | § 1.5 >> |
 является
равнодействующей силы притяжения
является
равнодействующей силы притяжения  и
силы инерции переносного движения (центробежной силы), возникающей вследствие
вращения Земли вокруг своей оси:
и
силы инерции переносного движения (центробежной силы), возникающей вследствие
вращения Земли вокруг своей оси:  .
.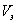 —
потенциал силы тяжести эллипсоидальной Земли;
—
потенциал силы тяжести эллипсоидальной Земли;  -
потенциал силы инерции переносного движения.
-
потенциал силы инерции переносного движения.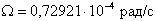


 (
( и плоскостью экватора.
и плоскостью экватора.
 и
на
и
на 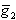 (
( противоположна
по направлению ранее полученной составляющей
противоположна
по направлению ранее полученной составляющей 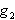 всегда
направлена к экватору.
всегда
направлена к экватору.