§ 1.2 Сила притяжения. Потенциал силы притяжения материальной точки, системы точек, тела произвольной формыСила притяжения Земли обусловливается законом всемирного тяготения, в
соответствии с которым две материальные частицы взаимно притягиваются с силой
Если притягивающая частица имеет массу |
|
где |
|
Притяжение материальной частицы Сила
Из теоретической механики известно, что указанная сила является
консервативной, т. е. имеющей силовую функцию, которую принято называть
ньютоновским потенциалом частицы с массой |
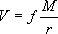 Функция координат точек поля, производная от которой по какому-либо направлению
равна проекции силы |
(1.6) |
|
Очевидно, что для направления, совпадающего с линией действия силы в данной точке поля, производная от потенциала максимальна и равна самой силе: 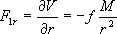 |
|
Это направление принято называть направлением линии потенциала данной точке. Знак в последнем выражении объяснялся противоположными направлениями действия силы притяжения и радиус-вектора, определяющего положение единичной массы, относительно притягивающей массы. |
|
Из выражения (1.6) видно, что потенциал поля в равноудаленных точках от притягивающей массы имеет одно и то же значение. Поверхность, проведенная через точки одинаковых потенциалов, называется эквипотенциальной поверхностью. Очевидно, что производная от потенциала по направлениям, перпендикулярным к линиям потенциала (по касательным к эквипотенциальным поверхностям), равна 0. |
|
Если притяжение создается не точечной массой, а системой материальных частиц, то потенциал такой системы равен сумме потенциалов притягивающих частиц: |
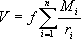 |
|
где |
|
Потенциал силы притяжения любого тела, в том числе и Земли, может быть представлен в виде: |
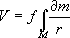 где |
(1.7) |
|
Интегрирование ведется по всей массе Земли. Выражение (1.7) нельзя использовать непосредственно для определения потенциала силы притяжения, так как неизвестно распределение массы в Земле, которое необходимо для практического вычисления интеграла. Поэтому для определения потенциала силы притяжения необходимо иметь дополнительное допущение о распределении массы Земли и о ее форме. |
| в начало | << § 1.1 | оглавление | § 1.3 >> |
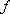 -
гравитационная постоянная;
-
гравитационная постоянная;
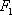 , с
которой она притягивает частицу единичной массы
, с
которой она притягивает частицу единичной массы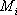 — масса
— масса  — расстояние от
— расстояние от