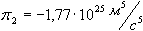§ 1.3 Потенциал силы притяжения для сферической и эллипсоидальной моделей землиПользуясь выражением 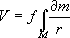 можно было бы записать выражение для потенциала силы притяжения Земли частицы единичной массы, равной потенциалу ускорения силы притяжения Земли. |
|
Однако вследствие сложности фигуры Земли и недостаточных знаний о распределении ее массы решение интеграла (1.7) для действительной формы Земли пока невозможно. Поэтому для решения практических задач вводятся упрощающие предположения относительно формы и распределения массы Земли. |
|
Для сферической модели Земли интеграл (1.7) вычисляется достаточно просто. Расчеты показывают, что сферическая Земля со сферическим распределением массы может быть заменена материальной точкой, в которой сосредоточена вся масса Земли. Потенциал силы притяжения сферической модели Земли равен |
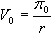
где |
(1.8) |
|
На основании изложенного, получим для сферической модели Земли: |
|
|
(1.9) |
|
— силу
притяжения, действующую на тело массой |
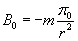 |
(1.10) |
|
Для эллипсоидной модели Земли (эллипсоида вращения, полученного вращением эллипса вокруг его малой оси) потенциал силы притяжения может быть с достаточным для практики приближением представлен выражением: |
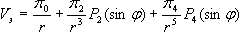 |
(1.11) |
|
|
|
В практических расчетах пользуются одним, двумя или тремя членами ряда в зависимости от дальности стрельбы. Мы будем пользоваться двумя членами ряда: |
 где |
(1.12) |
|
Из выражения (1.12)
видно, что потенциал силы притяжения эллипсоидальной Земли зависит не
только от величины текущего радиуса-вектора, но также от широты |
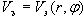 Выражение |
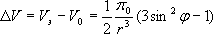 |
(1.13) |
|
дает возможность определить потенциал дополнительных сил притяжения эллипсоидальной Земли, то есть сил, которые нужно добавить к основной силе притяжения, чтобы получить силу притяжения, создаваемую более ложной моделью Земли. |
|
Так как
Направление |
|
Ускорения, сообщаемые притягиваемому телу силой притяжения в направлении осей
|
|
|
(1.14) |
|
|
(1.15) |
|
Пользуясь выражениями (1.14) и (1.15), можно получить составляющие силы притяжения, если каждое слагаемое указанных выражений помножить на массу БР. |
| в начало | << § 1.2 | оглавление | § 1.4 >> |
 = 3,9861679-1014
м3/с2;
= 3,9861679-1014
м3/с2;
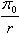 —
основной потенциал сферической модели Земли;
—
основной потенциал сферической модели Земли;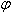 — геоцентрическая
широта текущей точки;
— геоцентрическая
широта текущей точки;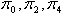 — постоянные,
характеризирующие поле притяжение Земли;
— постоянные,
характеризирующие поле притяжение Земли;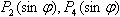 — полиномы Лежандра,
имеющие вид
— полиномы Лежандра,
имеющие вид