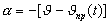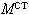§ 2.4 Уравнения плоского продольного движения и полетные свойства ЛА |
|
Движение ЛА на активном участке траектории и ее головной части на пассивном участке траектории представляет весьма сложный процесс. Характер и свойства этого процесса определяются многочисленными, часто противоречивыми факторами. Траектория полета является сложной пространственной кривой, весьма трудной для изучения. Точный анализ реальных проблем, связанных с таким движением, крайне сложен и моет быть проведен только путем численного решения сложных систем дифференциальных уравнений. Чаще всего среди факторов, которые определяют сложное движение ЛА, можно выделить основные. Их влияние на движение ЛА является определяющим. Остальные факторы можно отнести к второстепенным, так как их влияние на движение ЛА оказывается менее значительным. Поэтому изучение сложного движения ЛА целесообразно начинать с наиболее простой схемы, учитывающей действие только основных факторов. Движение ЛА, отвечающее такой простой схеме, обычно принимается за невозмущенное движение. Учет влияния второстепенных факторов на движение ЛА может быть проведен отдельно. Понятие невозмущенного движения является условным, что следует из условности деления факторов на основные и второстепенные. В этой главе будет рассмотрена схема плоского продольного движения, которая хорошо служит целям изучения основных закономерностей движения и поведения ЛА в полете. Анализ простой системы дифференциальных уравнений плоского движения позволяет более правильно понять сложную систему дифференциальных уравнений пространственного движения, механическое и физическое содержание теории полета. Для осмысливания получаемых результатов полезно также ввести понятия, поясняющие полетные свойства ЛА. Схема плоского продольного движения не может точно отразить все явления, сопровождающие полет ЛА. Для окончательного суждения по многим вопросам приходится привлекать более сложную схему движения ЛА. В этой главе будет рассмотрена одна из возможных схем пространственного невозмущенного полета, пригодная для решения различных практических задач теории полета. Векторные уравнения плоского продольного движения. |
| Рис. 2.4 |
Для рассмотрения плоского движения ЛА введем Земную систему координат Начало Земной системы координат расположено в точке старта Азимут рассчитывается перед пуском ЛА. Отсчет его проводится от северного направления касательной к меридиану в точке старта Условимся называть плоским продольным движением ЛА или движением в неподвижной вертикальной плоскости такое движение, при котором основная плоскость симметрии ЛА в течении всего времени полета совпадает с вертикальной плоскостью Движение ЛА будем рассматривать при следующих допущениях: 1. ЛА является абсолютно твердым осесимметричным телом, центр масс которого находится на продольной оси. 2. Земля принимается за тело сферической структуры радиусом 3. Вращение Земли вокруг своей оси не учитывается. 4. Параметры атмосферы соответствуют параметрам стандартной атмосферы. При этом положение ЛА в рассматриваемой плоскости полностью определяется, например, двумя полярными координатами Задача определения продольного движения ЛА сводится к определению для каждого момента времени параметров движения, например, 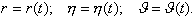 Как принято в механике, движение ЛА будем рассматривать, состоящим из поступательного движения вместе с центром масс и вращательного движения его вокруг центра масс. Применяя теорему о движении центра масс твердого тела к движению ЛА, запишем векторное уравнение |
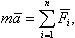 Здесь Уравнение (2.1) называют ещё уравнением сил. Применяя теорему об изменении момента количества движения твердого тела, запишем уравнение |
(2.1) |
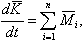 где |
(2.2) |
| Рис. 2.5 |
Необходимым условием осуществления ЛА продольного движения является отсутствие сил, перпендикулярных к плоскости движения ЛА и моментов относительно осей OX и OY. Условию осуществления продольного движения удовлетворяет основная сила притяжения Земли, так как она не дает составляющих, перпендикулярных к вертикальной плоскости |
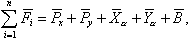 где Система моментов может быть представлена суммой |
(2.3) |
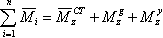 где После переноса всех сил в центр масс ЛА получим схему, изображенную на (Рис. 2.5). |
(2.4) |
|
Динамические уравнения Векторное уравнение (2.1) удобно спроектировать на оси скоростной системы координат. В этом случае проекции сил на ось |
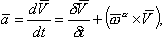 где Вектор По условию выбора направления осей скоростной системы координат всегда выполняются следующие равенства: |
(2.5) |
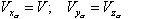 Для случая продольного движения проекции вектора угловой скорости вращения скоростной системы координат на оси этой же системы равны |
(2.6) |
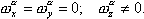 Представим векторное произведение |
(2.7) |
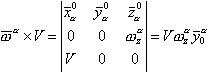 Вектор локальной производной Исходное векторное уравнение (2.1) можно теперь заменить скалярными уравнениями сил: |
(2.8) |
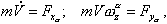 где Направление вектора скорости Из (Рис. 2.5) найдем проекции сил на оси скоростной системы координат и запишем уравнения (2.9) в следующем виде: |
(2.9) |
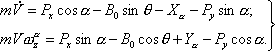 Уравнения движения ЛА относительно центра масс удобно рассматривать в связанной системе координат. При этом для рассматриваемых ЛА центробежные моменты инерции можно считать равными нулю и левые части уравнений движения записываются наиболее просто. Кроме того, орган управления создают моменты относительно осей связанной системы координат. Вектор момента количества движения в проекциях на оси связанной системы координат равен |
(2.10) |
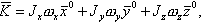 где В продольном движении рассматривается вращение ЛА только вокруг оси OZ. При этом проекция производной от момента количества движения равна произведению проекции углового ускорения |
(2.11) |
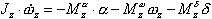 где В уравнениях (2.10), (2.12) масса, составляющие сил и градиенты моментов зависят от следующих параметров: 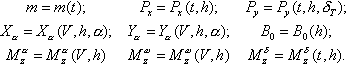 Таким образом, уравнения (2.10) и (2.12) содержат восемь неизвестных переменных величин Уравнения кинематических связей |
(2.12) |
| Рис. 2.6 |
Проектируя вектор скорости ЛА на направление радиуса и трансверсали (перпендикуляра к радиус-вектору), получаем (Рис. 2.6) Учитывая, что модули |
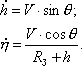 Кроме того, для продольного движения справедливы следующие отношения: |
(2.13) |
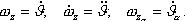 Уравнения геометрических связей Запишем простейшие геометрические соотношения, вытекающие из (Рис. 2.5), |
(2.14) |
| Рис. 2.7 |
В действительности угол отклонения органов управления определяется работой системы управления. Для простоты изложения будем пока считать, что ЛА снабжен только автоматом угловой стабилизации (АУС). Величина угла отклонения органов управления определяется работой канала тангажа АУС. Основные элементы канала тангажа АУС представлены на (Рис. 2.7). Программный элемент задает программное значение угла тангажа, который используется для управления полетом ЛА на активном участке траектории. В продольном движении углу тангажа соответствует угол 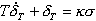 В приведенных формулах величины |
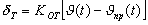 где Система уравнений Запишем в окончательном виде систему уравнений продольного движения ЛА в плоскости |
(2.16) |
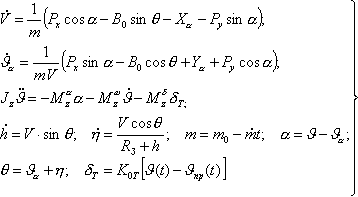 Неизвестными переменными являются Система уравнений (2.17) имеет шестой порядок. Для ее решения необходимо знать шесть начальных условий. Для  которые определяют движение ЛА в неподвижной вертикальной плоскости. Для решения системы уравнений (2.17) используются численные методы интегрирования. Среди ряда известных методов численного интегрирования наибольшее применение получили методы Рунге-Кутта и Адамса. Выбор величины шага интегрирования определяется необходимой точностью вычисления траектории полета ЛА. На активном участке траектории шаг интегрирования выбирается порядка 1-2 сек. Программа угла тангажа, характер изменения угла атаки Требуемое движение ЛА осуществляется в соответствии с заданными программными функциями управления или программами. |
(2.17) |
| Рис. 2.8 |
Рассмотрим возможный вид программы угла тангажа двухступенчатого ЛА. На (Рис. 2.8) изображены графики изменения программного значения угла тангажа |
| Рис. 2.9 |
Начальное постоянное значение угла тангажа |
| Рис. 2.10 |
Для изменения направления полёта ЛА должен под действием управляющего момента развернуться в вертикальной плоскости по направлению к цели (Рис. 2.10). Программное значение угла тангажа начинает уменьшаться. Так как в момент начала разворота корпуса ЛА вектор скорости сохраняет свое прежнее направление, возникает отрицательный угол атаки. При этом создается отрицательная нормальная управляющая сила По мере увеличения скорости движения ЛА увеличивается скоростной напор и пропорционально ему – аэродинамические силы. Для конструкции самого ЛА опасным является увеличение поперечных сил, в частности, подъемной силы. Чтобы свести к минимуму поперечные аэродинамические нагрузки в области околозвуковых скоростей, разворот по углу тангажа замедляется, и в дальнейшем полет до момента начала разделения ступеней проходит практически с нулевым углом атаки. К моменту разделения ступеней ЛА уже проходит область больших скоростных напоров. Однако для улучшения условий разделения ступеней желательно, чтобы в этот момент угол атаки был близок к нулю. После разделения ступеней программное значение угла тангажа быстро уменьшается до При развороте ЛА до величины угла |
| Рис. 2.11 |
В силу постоянства программного значения угла тангажа наклон продольной оси |
| Рис. 2.12 |
При положительном угле атаки нормальная управляющая сила Вид программы угла тангажа и соответственно характер изменения угла атаки для конкретного образца ЛА может значительно отличаться от указанного. Каждой программе угла тангажа соответствует своя траектория полета на активном участке траектории. Требования к программе угла тангажа Так как в некоторых пределах можно выбирать программу угла тангажа из большого числа возможных вариантов, то возникает вопрос о критериях, какими надлежит руководствоваться при выборе программ. Анализ особенностей конструкции ЛА, принятого вида старта, необходимых условий работы СУ позволяет определить ограничения, накладываемые на форму активного участка траектории. На основании данных такого анализа были сформулированы основные требования к программе тангажа. 1. Обеспечение наибольшей дальности полета. При решении этой задачи исходят из постоянного запаса топлива на борту ЛА, которое полностью расходуется на активном участке траектории. Необходимо иметь в конце активного участка такие параметры движения 2. Обеспечение минимального рассеивания. Наибольшая дальность полета вляется важной тактико-технической характеристикой. Однако часто это требование подчиняется требованию обеспечения минимального рассеивания. Наибольшая точность будет при больших углах входа ЛА (головной части) в плотные слои атмосферы. При этом приходится поступаться дальностью полета и выбирать такую траекторию, при которой можно получить минимальное рассеивание при дальности, незначительно отличающейся от максимальной . При решении этой задачи учитывается ещё ряд требований, связанных с условиями прочности ЛА, устойчивостью его полета, удобством эксплуатации и т.д. 3. Вертикальный старт и определенная продолжительность вертикального полета. Продолжительность вертикального полета определяется главным образом тем временем, которое необходимо для обеспечения устойчивого движения ЛА на начальном участке траектории. Продолжительность вертикального полета ЛА составляет 5-10 с. 4. Требование технической осуществимости программы. Приборы СУ и органы управления, реализующие программу угла тангажа на борту ЛА, имеют ограниченные возможности. Поэтому характер изменений функции 5. Обеспечение допустимых аэродинамических нагрузок. Нормальные (поперечные) перегрузки создаются силами, перпендикулярными к вектору скорости. Они зависят от величины угла атаки в первую очередь. Чтобы ЛА не разрушился, необходимо уменьшать угол атаки 6. Возможность осуществления пусков на любую дальность в заданном диапазоне дальностей с минимальным количеством программ. Для ЛА с широким диапазоном дальностей невозможно выбрать одну, достаточно удовлетворительную программу угла тангажа для всех дальностей. Приходится диапазон возможных дальностей разбивать на несколько более мелких диапазонов, т.е. увеличивать число программ на борту ЛА, что приводит к усложнению системы управления. 7. Обеспечение допустимого аэродинамического нагрева корпуса ЛА на АУТ. При движении ЛА со значительными скоростями в плотных слоях атмосферы увеличивается температура корпуса ЛА и его прочность уменьшается. Поэтому необходимо ограничивать область таких условий движения. 8. Обеспечение допустимого нагрева и перегрузок головной части при движении в плотных слоях атмосферы на ПУТ. Температура нагрева и аэродинамические перегрузки зависят от величин угла входа ГЧ в плотные слои атмосферы и скорости входа. При их увеличении температура нагрева и перегрузки увеличиваются. Поэтому задаются предельные значения угла и скорости полета. Как видим, требования, предъявляемые к программе угла тангажа, во многом противоречивы. Определение программы угла тангажа При выборе программы управления на активном участке в качестве критерия чаще всего рассматривается дальность полета головной части. Иногда ставится задача обеспечения минимального рассеивания. Одновременно должны учитываться все заданные ограничения на параметры траектории и режимы полета ЛА (например, по перегрузке, скоростному напору и т.п.). Рассмотрим задачу выбора программы угла тангажа, обеспечивающей максимальную дальность полета. Эта задача может быть сформулирована следующим образом. Для момента старта ЛА ( Этот вид соответствия в математике охватывается понятием функционала. При этом задача выбора программы угла тангажа, обеспечивающей наибольшую дальность полета, может быть представлена как задача определения такой функции Методы вариационного исчисления позволяют получить дополнительные дифференциальные уравнения, которые в совокупности с уравнениями движения дают возможность определить программу максимальной дальности как функции времени. Затем проверяется возможность удовлетворения требований минимального рассеивания, допустимых аэродинамических нагрузок и т.д. Выбор программы осуществляется здесь путем подбора или анализа полученных результатов. Изменяя значения параметров программы угла тангажа, добиваются получения такого движения ЛА на активном участке траектории, при котором выполняются сформулированные требования. Ускорение, кажущееся ускорение, перегрузка Рассмотрим величины, с помощью которых можно охарактеризовать суммарную силу, действующую на ЛА в полете. Из уравнения сил следует, что вектор ускорения |
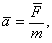 являясь величиной, прямо пропорциональной суммарной силе, служит её характеристикой. Проектируя равенство (2.18) на какие-либо направления, находят характеристики составляющих суммарной силы. Если, например, рассмотреть суммарную силу, действующую в направлении полета ЛА, то |
(2.18) |
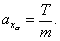
Касательное ускорение |
(2.19) |
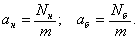 Для принятой схемы плоского продольного движения боковое ускорение равно нулю. |
(2.20) |
| Рис. 2.13 |
В автономных системах управления ускорения измеряются специальными приборами, называемыми акселерометрами. На примере простейшего акселерометра, представляющего собой инерциальную массу
Сначала рассмотрим ЛА, находящийся на пусковом столе (Рис. 2.13). Сила притяжения Справедливость сказанного можно проиллюстрировать известными в физике опытами профессора Любимова. |
| Рис. 2.14 |
На рамке, которая может без трения скользить по вертикальным направляющим, укрепляются на одинаковых пружинах два груза разной массы (Рис. 2.14). При закрепленной рамке грузы по-разному растягивают пружины. Когда освобожденная рамка свободно падает по направляющим, растяжение пружин исчезает. Таким образом, сила притяжения Земли действует на грузики при закрепленной и при свободно падающей рамке, а растяжение пружин наблюдается только в первом случае, когда на пружины действует реакция связи.
Аналогичное явление наблюдается на борту ЛА, совершающего свободный полет без сопротивления атмосферы. ЛА движется с ускорением
Итак, ЛА стоит на пусковом устройстве. Истинное ускорение |
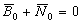 Из этого выражения получаем |
(2.21) |
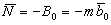 Следовательно, акселерометр замеряет ускорение |
(2.22) |
 Тогда векторное уравнение для кажущегося ускорения на основе данного определения представится следующим образом: |
(2.24) |
| Рис. 2.15 |
Для продольного движения ЛА проекцию |
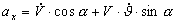 Проекция ускорения силы притяжения Земли на продольную ось определяется из того же чертежа:  В результате имеем |
(2.28) |
 или приближенно |
(2.29) |
| Рис. 2.16 |
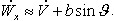 На активном участке траектории кажущееся ускорение больше истинного на величину проекции ускорения силы притяжения. Примерное соотношение между истинным и кажущимся ускорением в проекции на продольную ось показано на (Рис. 2.16). Продольное ускорение при движении ЛА растет вследствие увеличения тяги двигателя и уменьшения массы. Переход от первой ступени ко второй и связанные с этим изменения в режиме тяги вызывают скачкообразное уменьшение На участке разделения ступеней движущей силой является сила тяги рулевых двигателей. Ускорение При включении основных двигателей второй ступени ускорение На всем АУТ график продольного кажущегося ускорения Скорость. Кажущаяся скорость. К числу характеристик составляющей суммарной силы, действующей на ЛА в направлении ее полета, относится величина скорости центра масс. Если касательное ускорение характеризует суммарную силу, действующую на ЛА в полете в каждый текущий момент времени, то величина скорости характеризует действие суммарной силы за промежуток времени от начала полета до текущего момента времени. Скорость полета является важным параметром, значение которого в конце АУТ определяет в основном дальность полета головной части. От величины скорости в большой степени зависят значения аэродинамических сил, действующих на ЛА в полете. Из механики известно, что скорость движения любого тела определяется как интеграл от ускорения. Аналогичным образом вводится и понятие кажущейся скорости, представляющей интеграл от кажущегося ускорения. Например, на основании равенства (2.9) проекцию кажущейся скорости на направление продольной оси ЛА можно определить следующим образом: |
(2.30) |
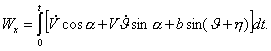 При малых дальностях полета ЛА на активном участке траектории и малых углах атаки можно использовать приближенную формулу: |
(2.31) |
 При малых дальностях полета ЛА на активном участке траектории и малых углах атаки можно использовать приближенную фрмулу: |
(2.32) |
| Рис. 2.17 |
Она следует из приближенного выражения (2.30). Характер изменений проекции векторов скорости центра масс ЛА Точка перегиба соответствует скачкообразному изменению проекций соответствующих ускорений в момент разделения ступеней. Интегралы, определяющие скорость движения и кажущуюся скорость, не могут быть выражены в общем случае конечными аналитическими формулами. Как правило, их определяют численными методами. Значение истинной скорости определяется по формуле 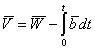 Например, значение скорости в проекции на ось ОХ равно Принципиальной особенностью автономной системы управления является определение скоростей и координат путем интегрирования измеренных значений кажущегося ускорения. Но из уравнения |
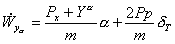 Из выражения (2.34) видно, что величина нормального ускорения Наряду с нормальным кажущимся ускорением на практике для оценки маневренности используется еще и нормальная перегрузка, определяемая равенством |
(2.34) |
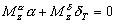 или |
(2.36) |
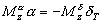 Разрешив это уравнение относительно угла атаки, получим балансировочную зависимость между углами атаки и углами отклонения органов управления |
(2.37) |
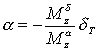 Найденная зависимость показывает, на какой угол атаки Отношение коэффициента управляющего момента к коэффициенту статического момента называется коэффициентом балансировки |
(2.38) |
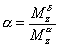 Как следует из выражений для моментов, |
(2.39) |
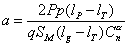 Введенная характеристика поворотливости справедлива для выбранного момента времени. Если ее относить к различным моментам времени движения ЛА на АУТ, то балансировочная зависимость оказывается связанной с выбранным движением центра масс. Введенная характеристика поворотливости справедлива для выбранного момента времени. Если ее относить к различным моментам времени движения ЛА на АУТ, то балансировочная зависимость оказывается связанной с выбранным движением центра масс. Коэффициент балансировки a претерпевает существенное изменение вдоль траектории. |
(2.40) |
| Рис. 2.18 |
На (Рис. 2.18) показан характер его изменения для одного из типов ЛА. Коэффициент управляющего момента изменяется незначительно. Поэтому характер кривой в основном определяется изменением коэффициента статического момента. Учет работы АУС не влияет на установленную выше балансировочную зависимость, так как АУС не добавляет новых сил и моментов, действующих на ЛА в полете. Однако работа АУС изменяет подход к обеспечению положения равновесия, определяемого равенством (2.39). Ранее угол |
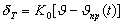 Из балансировочной зависимости (2.38) выразим |
(2.41) |
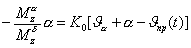 В левую часть уравнения перенесем слагаемые, пропорциональные углу атаки. В результате получим |
(2.42) |
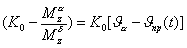
Обозначая |
(2.43) |
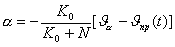 На больших высотах полета, где плотность воздуха пренебрежимо мала, коэффициент N=0, следовательно, |
(2.44) |
| Рис. 2.19a |
Если центр давления ЛА лежит позади центра масс, то ЛА статически устойчив (Рис. 2.19a). В этом случае при возникновении угла атаки появляется момент |
| Рис. 2.19b |
Если же центр давления лежит впереди центра масс, то возникающий при этом момент стремится увеличить возникший угол атаки, т.е. стремится как бы опрокинуть ЛА. Момент Однако у существующих типов ЛА корпус имеет такую конфигурацию и аэродинамическую форму, которые определяют расположение центра давления впереди центра масс на большей части АУТ. Следовательно, такие ЛА большую часть полета на АУТ являются статически неустойчивыми. Для обеспечения статической устойчивости, особенно на начальном участке полета ЛА, придают специальную форму (конусный хвостовой отсек) или используют на хвостовой части ЛА оперение. При этом центр давления перемещается (в полете) назад за центр масс. Для смещения центра масс ЛА вперед обычно бак окислителя помешается в переднюю часть корпуса. Кроме того, организуется расход топлива так, чтобы во время полета обеспечить смешение центра масс ближе к головной части. Для этого бак окислителя делят на полости и сначала окислитель расходуют из нижней полости, а затем из верхней. Устойчивое движение статически неустойчивого ЛА обеспечивается работой системы управления. |
| в начало | << § 2.3 | оглавление | § 2.5 >> |
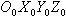


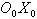
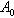
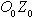
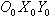
 (сферическая модель Земли).
(сферическая модель Земли).
 его центра масс и углом наклона продольной оси к плоскости
его центра масс и углом наклона продольной оси к плоскости  .
.
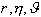 . Иначе говоря, задача сводится к определению функциональных зависимостей
. Иначе говоря, задача сводится к определению функциональных зависимостей
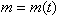 — масса ЛА.
— масса ЛА. 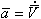 — ускорение центра масс ЛА в земной системе координат;
— ускорение центра масс ЛА в земной системе координат;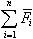 — сумма сил, действующих на ЛА в полете.
— сумма сил, действующих на ЛА в полете.
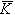 — вектор количества моментов движения (кинетический момент);
— вектор количества моментов движения (кинетический момент);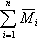 — сумма моментов, действующих на ЛА в полете.
— сумма моментов, действующих на ЛА в полете.
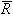 лежит в плоскости движения только при условии равенства боковой силы нулю. Значит, продольное движение должно рассматриваться происходящим без угла скольжения. При этом
лежит в плоскости движения только при условии равенства боковой силы нулю. Значит, продольное движение должно рассматриваться происходящим без угла скольжения. При этом 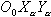
 . В рассматриваемом случае движения ЛА сумма сил, действующих на ЛА в полете
. В рассматриваемом случае движения ЛА сумма сил, действующих на ЛА в полете
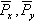 — проекции силы тяги двигателя
— проекции силы тяги двигателя связанной системы координат;
связанной системы координат;  — проекции вектора полной аэродинамической силы
— проекции вектора полной аэродинамической силы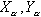 скоростной системы координат;
скоростной системы координат;  — статический аэродинамический момент,
— статический аэродинамический момент, 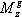 — демпфирующий момент,
— демпфирующий момент, 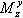 — управляющий момент.
— управляющий момент.
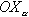 будут изменять только величину
будут изменять только величину 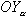 будут изменять только направление вектора скорости, не меняя его величины. Так как скоростная система координат является подвижной системой, то полное ускорение
будут изменять только направление вектора скорости, не меняя его величины. Так как скоростная система координат является подвижной системой, то полное ускорение 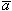 в земной системе координат на основании теоремы о полной и относительной (локальной) производной от вектора следует представить в следующем виде
в земной системе координат на основании теоремы о полной и относительной (локальной) производной от вектора следует представить в следующем виде
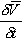 — локальная или относительная производная, которая характеризует быстроту изменения
— локальная или относительная производная, которая характеризует быстроту изменения 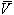
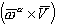 определяет быстроту изменения вектора за счёт вращения самой скоростной системы координат с угловой скоростью
определяет быстроту изменения вектора за счёт вращения самой скоростной системы координат с угловой скоростью 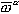 относительно осей основной системы координат.
относительно осей основной системы координат.
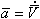 называется полным ускорением. Он характеризует быстроту изменения
называется полным ускорением. Он характеризует быстроту изменения  , поэтому проекция вектора ускорения на эту ось равна
, поэтому проекция вектора ускорения на эту ось равна 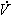 .
.
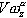 — нормальное ускорение;
— нормальное ускорение; 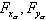 — проекции суммарной силы соответственно на оси
— проекции суммарной силы соответственно на оси 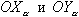 .
.
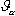 , который заключен между вектором
, который заключен между вектором 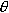 и называется углом бросания.
и называется углом бросания.
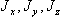 — моменты инерции ЛА относительно осей связанной системы координат;
— моменты инерции ЛА относительно осей связанной системы координат; 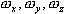 — проекции угловой скорости вращения ЛА на оси связанной системы координат;
— проекции угловой скорости вращения ЛА на оси связанной системы координат; 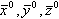 — единичные векторы, направленные по соответствующим осям связанной системы координат.
— единичные векторы, направленные по соответствующим осям связанной системы координат.
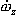 на момент инерции ракеты относительно оси OZ. Уравнение (2.2) в проекции на ось OZ записывается в виде
на момент инерции ракеты относительно оси OZ. Уравнение (2.2) в проекции на ось OZ записывается в виде
 — коэффициенты (градиенты) статического демпфирующего и управляющего моментов, введенные в
— коэффициенты (градиенты) статического демпфирующего и управляющего моментов, введенные в 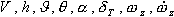 . Эти уравнения не могут еще однозначно определять продольное движения ЛА, так как число неизвестный переменных величин превосходит число уравнений. Вместе с тем основные теоремы динамики твердого тела уже использованы. Следовательно, не все, перечисленные неизвестные, являются независимыми. Для «замыкания» системы необходимо добавить уравнения, выражающие связь между неизвестными переменными.
. Эти уравнения не могут еще однозначно определять продольное движения ЛА, так как число неизвестный переменных величин превосходит число уравнений. Вместе с тем основные теоремы динамики твердого тела уже использованы. Следовательно, не все, перечисленные неизвестные, являются независимыми. Для «замыкания» системы необходимо добавить уравнения, выражающие связь между неизвестными переменными.
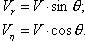
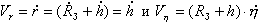
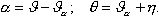
 .
. 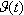 и его программным значением
и его программным значением 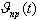 . На выходе элемента выделяется первичный сигнал
. На выходе элемента выделяется первичный сигнал 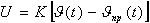 . Он поступает в
. Он поступает в 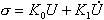 или
или 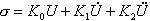 .
. 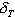
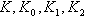 — представляют собой коэффициенты пропорциональности; T — постоянная времени;
— представляют собой коэффициенты пропорциональности; T — постоянная времени; 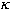 — коэффициент усиления. В установившемся режиме работа канала тангажа описывается статическим уравнением
— коэффициент усиления. В установившемся режиме работа канала тангажа описывается статическим уравнением
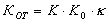 — статический коэффициент усиления канала.
— статический коэффициент усиления канала.
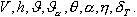 . Величины
. Величины 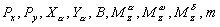 являются известными функциями времени и неизвестных переменных. Они определяются по формулам, приведенным в
являются известными функциями времени и неизвестных переменных. Они определяются по формулам, приведенным в 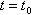 должны быть заданы
должны быть заданы 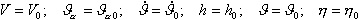 . В результате интегрирования системы отыскиваются функции
. В результате интегрирования системы отыскиваются функции
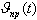
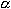
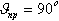
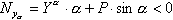 , которая вызовет отклонение центра масс ЛА в сторону цели.
, которая вызовет отклонение центра масс ЛА в сторону цели.
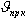 . Дальнейший полет второй ступени происходит практически в безвоздушном пространстве с постоянным углом тангажа. Как при этом меняется угол атаки?
. Дальнейший полет второй ступени происходит практически в безвоздушном пространстве с постоянным углом тангажа. Как при этом меняется угол атаки?
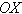
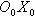 основной системы координат
основной системы координат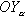 скоростной системы отлична от нуля и продолжает искривлять траекторию.
скоростной системы отлична от нуля и продолжает искривлять траекторию. 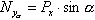
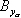
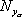 и проекции силы притяжения
и проекции силы притяжения 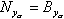 рост
рост 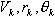 , которые могли бы обеспечить наибольшую дальность полета. При фиксированных значениях
, которые могли бы обеспечить наибольшую дальность полета. При фиксированных значениях  наибольшую дальность полета можно получить для вполне определенного значения
наибольшую дальность полета можно получить для вполне определенного значения 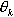 , равного углу бросания максимальной дальности
, равного углу бросания максимальной дальности 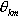 .
.
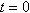 ) заданы начальные условия движения
) заданы начальные условия движения 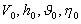 и задан момент включения двигателя
и задан момент включения двигателя 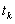 . При решении задачи выбора программы угла тангажа
. При решении задачи выбора программы угла тангажа 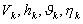 . Каждому сочетанию параметров движения
. Каждому сочетанию параметров движения 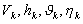 в конце активного участка отвечает определенное значение дальности полета
в конце активного участка отвечает определенное значение дальности полета 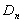 . Получается новый вид соответствия: каждой новой функции
. Получается новый вид соответствия: каждой новой функции 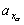 служит характеристикой составляющей суммарной силы, действующей в направлении движения ЛА (продольное). Перпендикулярные к вектору скорости (поперечные ) составляющие суммарной силы характеризуются нормальным
служит характеристикой составляющей суммарной силы, действующей в направлении движения ЛА (продольное). Перпендикулярные к вектору скорости (поперечные ) составляющие суммарной силы характеризуются нормальным 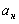 и боковым
и боковым 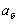 ускорениями, под которыми понимают проекции ускорения на направления нормали и бинормали к траектории:
ускорениями, под которыми понимают проекции ускорения на направления нормали и бинормали к траектории:
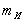 , подвешенную на пружине
, подвешенную на пружине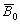
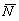
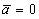 . Такая же по физической природе сила действует на пружину в точке ее крепления к корпусу ЛА. При этом пружина растягивается и в определенном масштабе фиксирует ускорение. Наблюдается объективно существующее несоответствие между показаниями акселерометра и ускорением ЛА. Это несоответствие возникает потому, что инерциальные измерители не реагируют на изменение силы притяжения. В данном случае он ускорение от силы реакции, численно равное ускорению земного притяжения.
. Такая же по физической природе сила действует на пружину в точке ее крепления к корпусу ЛА. При этом пружина растягивается и в определенном масштабе фиксирует ускорение. Наблюдается объективно существующее несоответствие между показаниями акселерометра и ускорением ЛА. Это несоответствие возникает потому, что инерциальные измерители не реагируют на изменение силы притяжения. В данном случае он ускорение от силы реакции, численно равное ускорению земного притяжения.
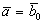 под действием силы притяжения земли. Одинаково действующая и на корпус, и на акселерометр сила притяжения не вызывает растяжение пружины.
под действием силы притяжения земли. Одинаково действующая и на корпус, и на акселерометр сила притяжения не вызывает растяжение пружины.
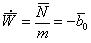
 называют ускорение, создаваемое всеми действующими на него силами, за исключением силы притяжения земли. Иначе, это ускорение, создаваемое поверхностными силами.
называют ускорение, создаваемое всеми действующими на него силами, за исключением силы притяжения земли. Иначе, это ускорение, создаваемое поверхностными силами.
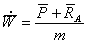
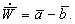
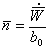
 и нормали
и нормали 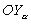 к траектории называют соответственно касательной и нормальной перегрузками.
к траектории называют соответственно касательной и нормальной перегрузками.
 оси чувствительности
оси чувствительности 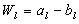 . Например, измеритель, ось чувствительности которого совмещена с продольной осью ЛА, измеряет продольное кажущееся ускорение
. Например, измеритель, ось чувствительности которого совмещена с продольной осью ЛА, измеряет продольное кажущееся ускорение 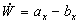 .
.
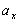 легко найти проектированием касательного и нормального ускорений на ось
легко найти проектированием касательного и нормального ускорений на ось 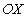 . Из
. Из 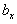 и аэродинамической силы
и аэродинамической силы 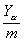 превышают ускорение ото всех остальных сил.
превышают ускорение ото всех остальных сил.
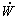 (пунктирная линия)
(пунктирная линия) 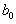 . Далее она изменяется по закону
. Далее она изменяется по закону  . Поскольку угол
. Поскольку угол 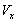
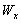
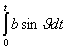 .
.
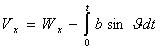 , т.е. значение истинной скорости меньше значения кажущейся скорости на величину
, т.е. значение истинной скорости меньше значения кажущейся скорости на величину  . Введенные понятия кажущегося ускорения и кажущейся скорости играют важную роль в методах управления движением ЛА, реализуемых автономными системами управления. Как было уже указано, измерители (акселерометры) замеряют кажущееся ускорение. Вместе с тем в задачу СУ входит и вычисление истинных параметров движения в заданной системе координат.
. Введенные понятия кажущегося ускорения и кажущейся скорости играют важную роль в методах управления движением ЛА, реализуемых автономными системами управления. Как было уже указано, измерители (акселерометры) замеряют кажущееся ускорение. Вместе с тем в задачу СУ входит и вычисление истинных параметров движения в заданной системе координат.
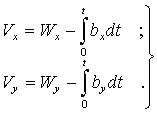
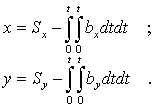
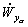 является функцией углов
является функцией углов 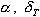 . Если эти углы равны нулю, то ЛА совершает движение по криволинейной траектории, называемой баллистической траекторией. Искривление траектории происходит под действием силы притяжения Земли, которая для управления полетом не используется. Нормальное ускорение
. Если эти углы равны нулю, то ЛА совершает движение по криволинейной траектории, называемой баллистической траекторией. Искривление траектории происходит под действием силы притяжения Земли, которая для управления полетом не используется. Нормальное ускорение 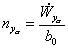
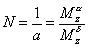 , перепишем полученное уравнение в окончательном виде:
, перепишем полученное уравнение в окончательном виде: